It consists on a new method to automatically extract all fuzzy parameters of a Fuzzy Logic Controller (FLC) in order to control nonlinear industrial processes. The main objective is the extraction of a FLC from data extracted from a given process while it is being manually controlled.
In general, it is not easy to determine the most suitable fuzzy rules and membership functions to control the output of a plant, when the only available knowledge concerning the process is the empirical information transmitted by a human operator. Thus, a major challenge in current fuzzy control research is translating human empirical knowledge into FLCs. A possible candidate to meet this challenge is the application of the genetic algorithm (GA) approach to data extracted from a given process while it is being manually controlled.
Previous methods only optimize membership function parameters, considering the other components of the fuzzy system fixed, such as implication, aggregation and defuzzifier methods. Other common limitation is the selection of the correct set of input variables and delays. The variable selection process is usually either manual, or made by some auxiliary pre-selection criterion, and is not accompanied with the accurate selection of the right time delays, probably leading to low-accuracy results. A variable with the correct delay may contain more information about the output, than one which does not consider any delay. However, the variable and delay selection are not jointly performed with the learning of the fuzzy model, which precludes the global optimization of the prediction setting.
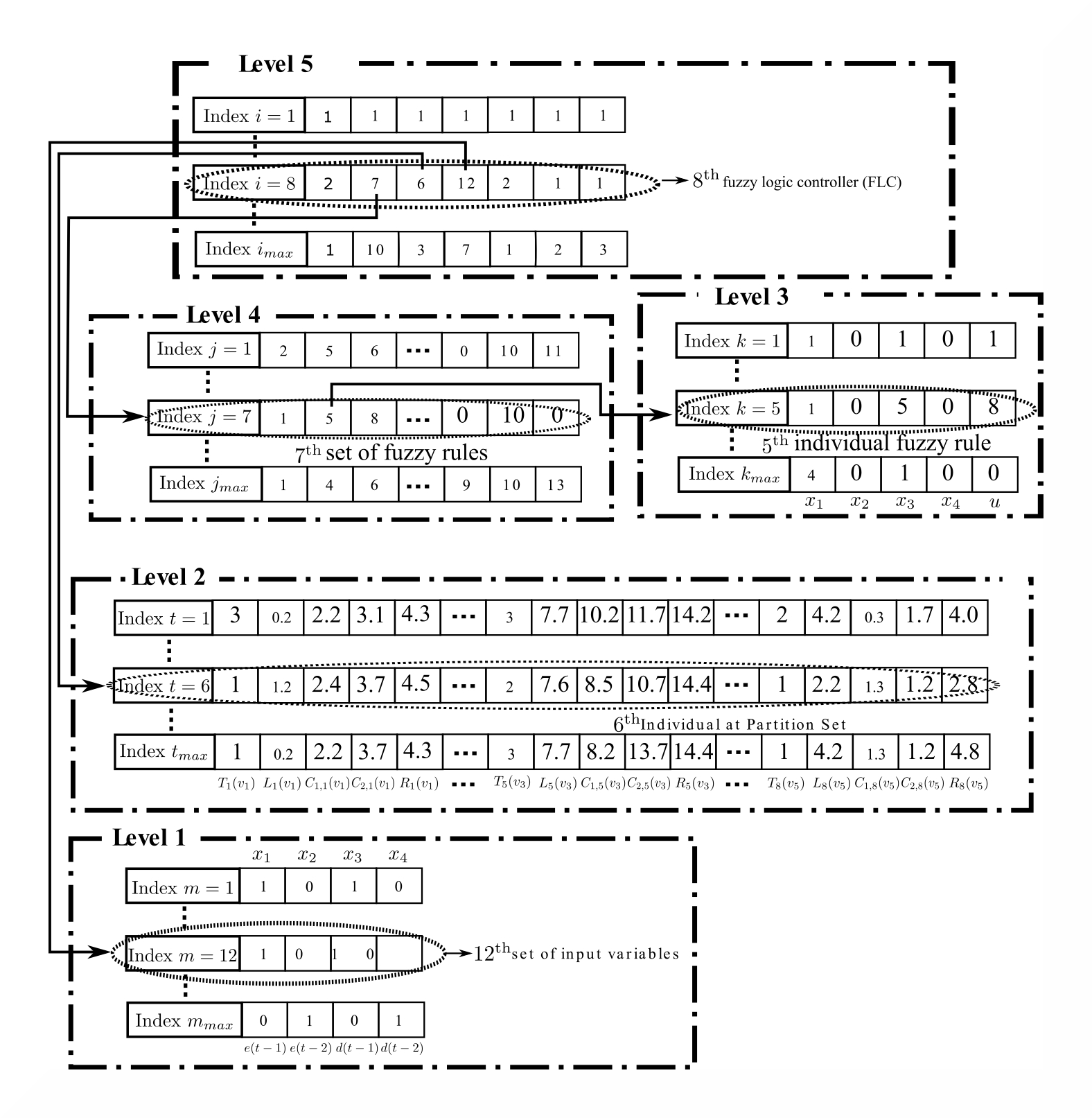
In this method, all the components of a standard fuzzy control system (FCS) are jointly optimized in order to extract the fuzzy control rules, and the FCS in general. The learning of the FLC is performed by a hierarchical genetic algorithm (HGA), from a set of process-controlled input/output data. The algorithm is composed of a five level structure, being the first level responsible for the selection of an adequate set of input variables. The second level considers the encoding of the membership functions. The individual rules are defined on the third level. The set of rules are obtained on the fourth level, and finally, the fifth level selects the elements of the previous levels, as well as, the t-norm operator, inference engine and defuzzifier methods which constitute the FLC.
To optimize the proposed method, the HGA's initial populations are obtained by an initialization algorithm. This algorithm has the main goal of providing a good initial solution for membership functions and rule-based populations, enhancing the GA's tuning.
The HGA is applied to control the dissolved oxygen in an activated sludge reactor within a wastewater treatment plant. The results show that the proposed method extracted all parameters of the fuzzy controller, successfully controlling a nonlinear plant.